思路:双指针
对于给定的非负整数 \(c\),需要判断是否存在整数 \(a\) 和 \(b\),使得 \(a^2+b^2=c\)。可以枚举 \(a\) 和 \(b\) 所有可能的情况,时间复杂度为 \(O(c^2)\)。但是暴力枚举有一些情况是没有必要的。例如:当
\(c=20\) 时,当 \(a=1\) 的时候,枚举 \(b\) 的时候,只需要枚举到 \(b=5\) 就可以结束了,这是因为 \(1^2+5^2=25>20\)。当 \(b>5\) 时,一定有 \(1^2+b^2>20\)。
假设 \(a\leq b\),初始时 \(a=0\),\(b=\sqrt
c\),进行如下操作:
- 如果 \(a^2+b^2=c\),我们找到了题目要求的一个解,直接返回
true;
- 如果 \(a^2+b^2<c\),此时需要将
\(a\) 的值加 \(1\),继续查找;
- 如果 \(a^2+b^2>c\),此时需要将
\(b\) 的值减 \(1\),继续查找。
当 \(a=b\)
时,结束查找,此时如果仍然没有找到整数 \(a\) 和 \(b\) 满足 \(a^2+b^2=c\),则说明不存在题目要求的解,返回
false。
class Solution {
public:
bool judgeSquareSum(int c)
{
int left = 0, right = sqrt(c);
while(left <= right)
{
long long res = (long long)left*left + (long long)right*right;
if(res < c)
{
left++;
}
else if(res > c)
{
right--;
}
else
{
return true;
}
}
return false;
}
};
|
- 时间复杂度:\(O(\sqrt
c)\)
- 空间复杂度:\(O(1)\)
思路:
题目相当于从数组中选两个数,我们只关心这两个数的和是否小于 \(target\),由于 \(a+b=b+a\),无论如何排列数组元素,都不会影响加法的结果,所以排序不影响答案。比如
\(nums=[1,2]\), \(target=4\) 和 \(nums=[2,1]\), \(target=4\) 算出来的答案都是 \(1\),可见排序并不影响结果。
排序后:
初始化左右指针 \(left=0\), \(right=n−1\)。 如果 \(nums[left]+nums[right]<target\),由于数组是有序的,\(nums[left]\) 与下标 \(i\) 在区间 \([left+1,right]\) 中的任何 \(nums[i]\) 相加,都是 \(<target\) 的,因此直接找到了 \(right−left\) 个合法数对,加到答案中,然后将
left 加一。 如果 \(nums[left]+nums[right]≥target\),由于数组是有序的,\(nums[right]\) 与下标 i 在区间 \([left,right−1]\) 中的任何 \(nums[i]\) 相加,都是 \(≥target\) 的,因此后面无需考虑 \(nums[right]\),将 \(right\) 减一。 重复上述过程直到 \(left≥right\) 为止。
class Solution {
public:
int countPairs(vector<int>& nums, int target)
{
int n = nums.size();
int left = 0, right = n-1;
sort(nums.begin(), nums.end());
int ans = 0;
while(left < right)
{
int sum = nums[left] + nums[right];
if(sum >= target) right--;
else
{
ans += (right-left);
left++;
}
}
return ans;
}
};
|
- 时间复杂度:\(O(n log
n)\)(由排序决定)
- 空间复杂度:\(O(log
n)\)(由排序的递归栈空间决定)
思路:两次相向双指针
class Solution {
public:
long long countFairPairs(vector<int>& nums, int lower, int upper)
{
int n = nums.size();
sort(nums.begin(), nums.end());
long long ans_temp = 0;
int left = 0, right = n-1;
while(left < right)
{
int sum = nums[left] + nums[right];
if(sum >= lower)
{
right--;
}
else
{
ans_temp += (right-left);
left++;
}
}
left = 0; right = n-1;
while(left < right)
{
int sum = nums[left] + nums[right];
if(sum <= upper)
{
left++;
}
else
{
ans_temp += (right-left);
right--;
}
}
return (long long)n*(n-1)/2-ans_temp;
}
};
|
- 时间复杂度:\(O(nlogn)\),其中 \(n\) 为 \(nums\) 的长度。瓶颈在排序上。
- 空间复杂度:\(O(1)\)。忽略排序的栈开销。
15. 三数之和
思路1 :排序+哈希表
class Solution {
public:
vector<vector<int>> threeSum(vector<int>& nums)
{
int n = nums.size();
sort(nums.begin(), nums.end());
vector<vector<int>> ans;
for(int i = 0; i < n-2; ++i)
{
int target = -1*nums[i];
if(i && nums[i] == nums[i-1]) continue;
unordered_set<int> cnt;
for(int j = i+1; j < n; ++j)
{
if(cnt.count(target-nums[j]))
{
ans.push_back({nums[i], nums[j], target-nums[j]});
while (j+1 < n && nums[j] == nums[j + 1]) j++;
}
cnt.insert(nums[j]);
}
}
return ans;
}
};
|
- 时间复杂度:\(O(n²)\)(外层循环 \(O(n)\),内层循环 \(O(n)\))。
- 空间复杂度:\(O(n)\)(哈希表存储 \(nums[j]\))。
思路2:排序+双指针
class Solution {
public:
vector<vector<int>> threeSum(vector<int>& nums)
{
int n = nums.size();
sort(nums.begin(), nums.end());
vector<vector<int>> ans;
for(int i = 0; i < n-2; ++i)
{
int target = -1*nums[i];
if(i && nums[i] == nums[i-1]) continue;
int left = i+1, right = n-1;
while(left < right)
{
int res = nums[left] + nums[right];
if(res < target)
{
left++;
}
else if(res > target)
{
right--;
}
else
{
ans.push_back({nums[i], nums[left], nums[right]});
while(left < right && nums[left] == nums[left+1]) left++;
while(left < right && nums[right] == nums[right-1]) right--;
left++;right--;
}
}
}
return ans;
}
};
|
思路:动态规划
如果 \(k=1\),那就是 53.
最大子数组和。注意本题允许子数组为空,答案最小是 \(0\),不可能是负数。
如果 \(k=2\),我们计算的是 \(arr+arr\) 的最大子数组和。直接调用 53
题的代码。
如果 \(k≥3\) 呢?
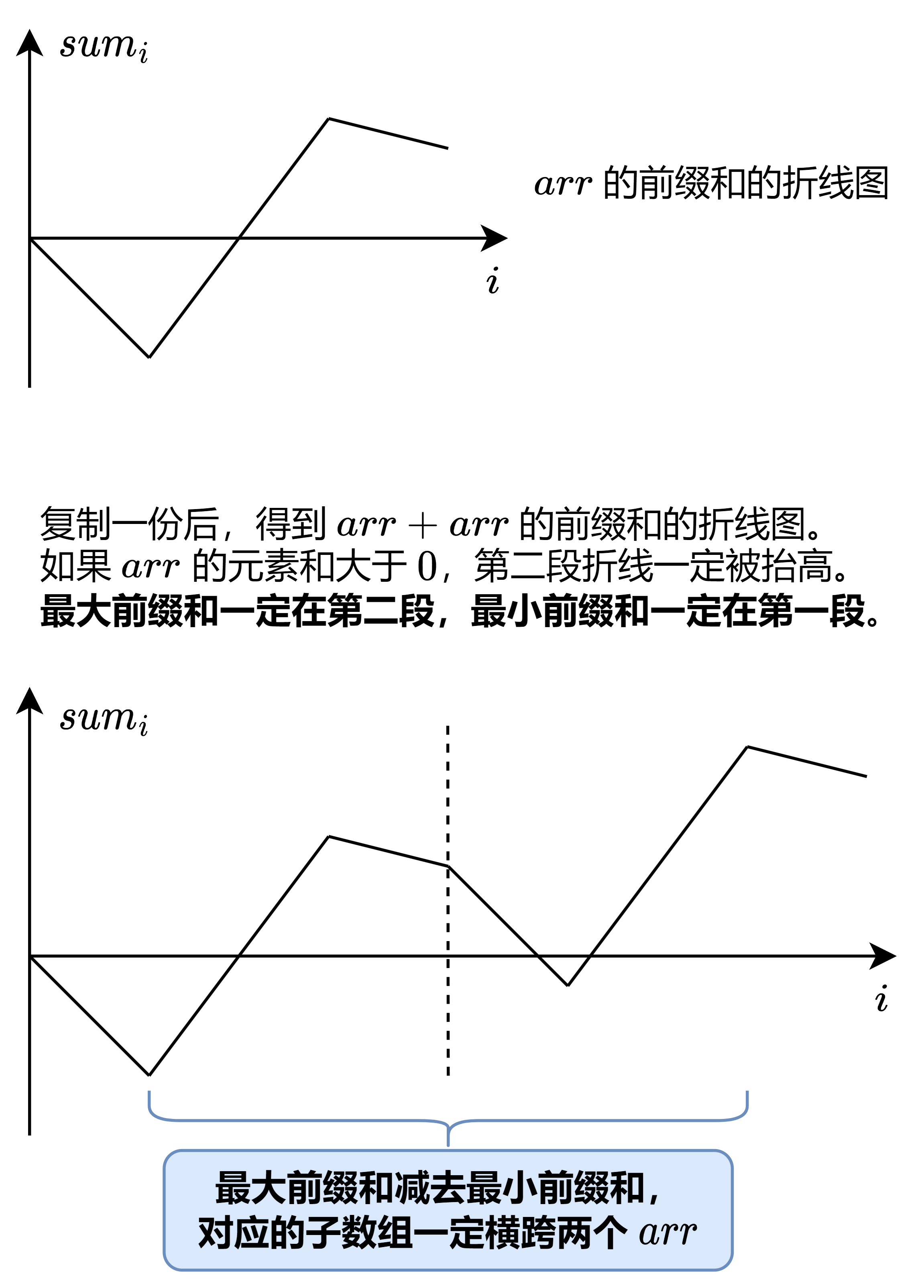
定理:设 \(s\) 是 \(arr\) 的元素和。如果 \(s>0\),那么 \(arr+arr\) 的最大子数组和必然横跨两个 \(arr\),不会在其中一个 \(arr\) 中间。
证明:如果 \(s>0\),那么前缀和的最大值一定在第二段,前缀和的最小值一定在第一段,所以最大前缀和减去最小前缀和,对应的子数组一定横跨两个
arr。如下图。
所以我们只需要计算 \(arr+arr\)
的最大子数组和。如果 \(s>0\),那么答案额外增加 \(s⋅(k−2)\)。相当于在 \(arr+arr\) 的最大子数组和中间插入 \(k−2\) 个完整的 \(arr\)。
class Solution {
public:
int kConcatenationMaxSum(vector<int>& arr, int k)
{
if(k == 1) return maxSubArray(arr);
vector<int> nums(arr);
nums.insert(nums.end(), arr.begin(), arr.end());
long long maxSub = maxSubArray(nums);
long long sum = reduce(arr.begin(), arr.end());
const int MOD = 1'000'000'007;
if(sum > 0)
{
return (maxSub + (k-2)*sum)%MOD;
}
return maxSub;
}
private:
int maxSubArray(vector<int>& nums)
{
int n = nums.size();
int maximum = 0, ans = 0;
for(int i = 0; i < n; ++i)
{
maximum = max(maximum+nums[i], nums[i]);
ans = max(ans, maximum);
}
return ans;
}
};
|
- 时间复杂度:\(O(n)\),其中 \(n\) 是 \(arr\) 的长度。
- 空间复杂度:\(O(n)\) 或 \(O(1)\)。取决于实现。