每周LeetCode回顾-1

73. 矩阵置零

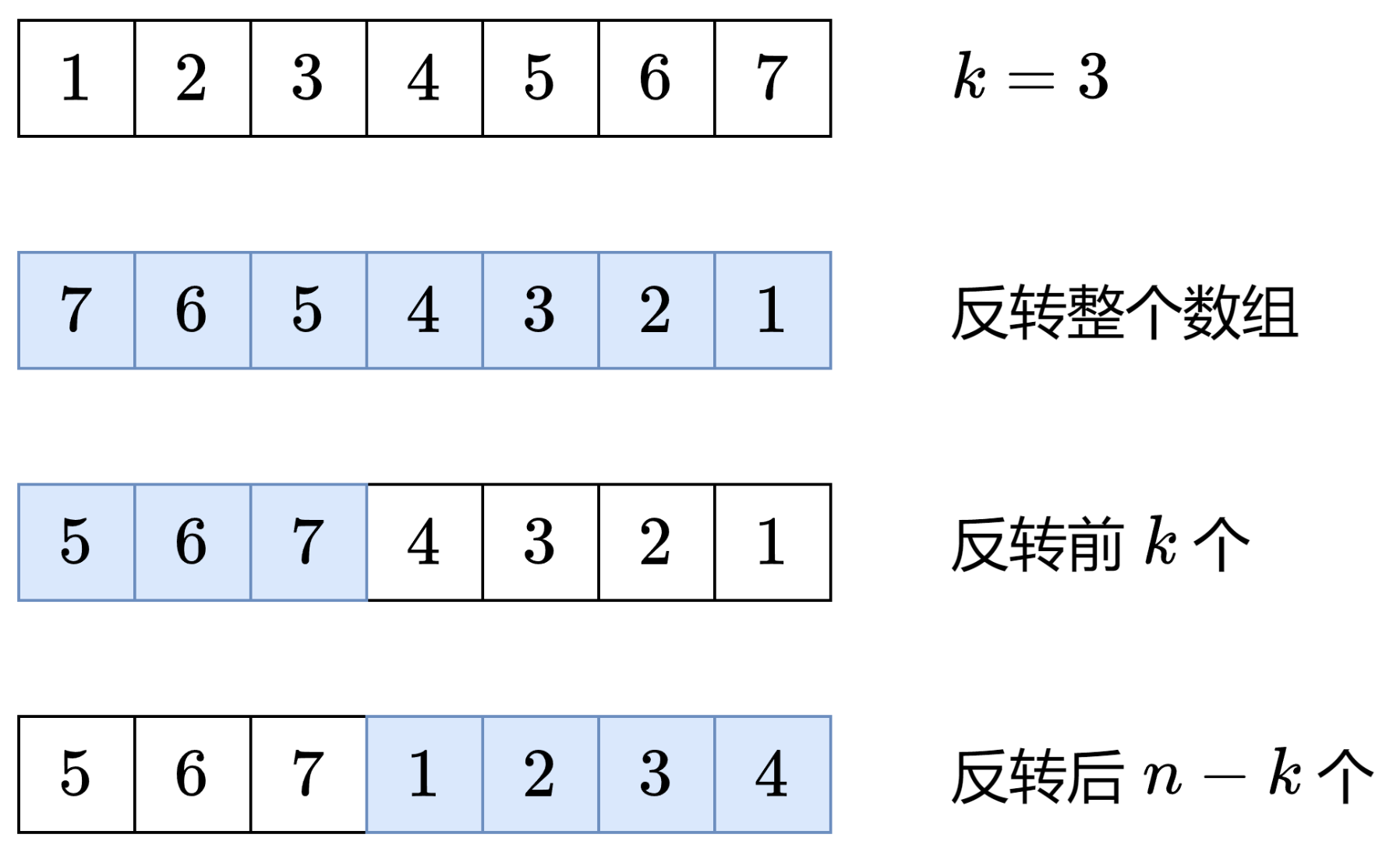
思路：

使用与行列数量相等的数组记录置零信息。

class Solution {
public:
    void setZeroes(vector<vector<int>>& matrix) 
    {
        // 行数
        int m = matrix.size();
        // 列数
        int n = matrix[0].size();
        // 记录置零位置
        vector<int> cols(n);
        vector<int> rows(m);
        // 遍历矩阵，寻找置零位置
        for(int i = 0; i < m; ++i)
        {
            for(int j = 0; j < n; ++j)
            {
                if(matrix[i][j] == 0)
                {
                    rows[i] = 1;
                    cols[j] = 1;
                }
            }
        }
        // 遍历矩阵将记录的行和列置零
        for(int i = 0; i < m; ++i)
        {
            for(int j = 0; j < n; ++j)
            {
                if(rows[i] == 1 || cols[j] == 1)
                {
                    matrix[i][j] = 0;
                }
            }
        }
    }
};

时间复杂度：O(m × n)
空间复杂度：O(m + n)

1297. 子串的最大出现次数

思路：

只需统计长度为 minSize 的子串，而不需要统计长度为 maxSize 的字串，因为 “abc” 肯定会覆盖 “a”，“ab”，即长的肯定会覆盖短的，只需要考虑最短的即可。

class Solution {
public:
    int maxFreq(string s, int maxLetters, int minSize, int maxSize) 
    {
        int n = s.size(), ans = 0;
        // 统计子串出现的次数
        unordered_map<string, int> cnt;
        for(int i = 0; i < n-minSize+1; ++i)
        {
            // 获取子串（定长滑动窗口）
            string subString = s.substr(i, minSize);
            // 利用哈希集合统计不同字母的个数
            unordered_set<int> hash_set(subString.begin(), subString.end());
            // 如果满足不同字母数目小于等于 maxLetters
            if(hash_set.size() <= maxLetters)
            {
                // 当前子串个数++
                cnt[subString]++;
                // 尝试更新最长子串
                ans = max(ans, cnt[subString]);
            }
        }    
        return ans;
    }
};

时间复杂度：**O(n*minSize)**
空间复杂度：**O(n*minSize)**

2389. 和有限的最长子序列

思路：

贪心：由于元素和有上限，为了能让子序列尽量长，子序列中的元素值越小越好。

对于本题来说，元素在数组中的位置是无关紧要的（因为我们计算的是元素和），所以可以排序了。把 nums 从小到大排序后，再从小到大选择尽量多的元素（相当于选择一个前缀），使这些元素的和不超过询问值。

既然求的是前缀的元素和（前缀和），那么干脆把每个前缀和都算出来。做法是递推：前 i 个数的元素和，等于前 i−1 个数的元素和，加上第 i 个数的值。

例如 [4,5,2,1] 排序后为 [1,2,4,5]，从左到右递推计算前缀和，得到 [1,3,7,12]。

由于 nums[i] 都是正整数，前缀和是严格单调递增的，这样就能在前缀和上使用二分查找：找到大于 queries[i] 的第一个数的下标，由于下标是从 0 开始的，这个数的下标正好就是前缀和小于等于 queries[i] 的最长前缀的长度。

例如在 [1,3,7,12] 二分查找大于 3 的第一个数（7），得到下标 2，这正好就是前缀和小于等于 3 的最长前缀长度。对应到 nums 中，就是选择了 2 个数（1 和 2）作为子序列中的元素。

class Solution {
public:
    vector<int> answerQueries(vector<int>& nums, vector<int>& queries) 
    {
        int n = nums.size(), m = queries.size();

        // 由于题目只要求子序列，所以可以对原数组进行排序
        sort(nums.begin(), nums.end());

        // 计算元素前缀和
        // 可以使用 C++ 函数 partial_sum(nums.begin(), nums.end()) 原地求前缀和
        vector<int> preSum(n);
        preSum[0] = nums[0];
        for(int i = 1; i < n; ++i)
        {
            preSum[i] = preSum[i-1]+nums[i];
        }    

        vector<int> ans;
        for(int i = 0; i < m; ++i)
        {
            // lower_bound 找到第一个 <= 的元素
            // upper_bound 找到第一个 < 的元素，会覆盖所有 <= 的元素
            auto it = upper_bound(preSum.begin(), preSum.end(), queries[i]);
            // 计算元素个数
            ans.emplace_back(it-preSum.begin());
        }

        return ans;
    }
};

时间复杂度：O((n + m) log n)
空间复杂度：O(n + m)

2606. 找到最大开销的子字符串

思路：

按照题目要求，把 s 中的字母映射到数字上，设映射后变成了数组 a，那么题目相当于求 a 的 53.最大子数组和（允许子数组为空）。

定义 dp[i] 为以 a[i] 结尾的最大子数组和，考虑是否接在以 a[i−1] 结尾的最大子数组之后：

接：\(dp[i]=dp[i−1]+a[i]\)
不接：\(dp[i]=a[i]\)

二者取最大值，得 \[ dp[i]=max(dp[i−1],0)+a[i] \] 答案为 \(max(dp)\)。

class Solution {
public:
    int maximumCostSubstring(string s, string chars, vector<int>& vals) 
    {
        int n = chars.size();

        // 记录特殊字母对应的开销
        unordered_map<char, int> valueTable;
        for(int i = 0; i < n; ++i)
        {
            valueTable[chars[i]] = vals[i];
        }    

        int m = s.size();
        // 初始化 dp 数组
        vector<int> dp(m);
        dp[0] = s[0]-'a'+1;
        if(valueTable.count(s[0])) dp[0] = valueTable[s[0]];
        // 最大开销的初始值
        int ans = dp[0];
        for(int i = 1; i < m; ++i)
        {
            int value = s[i]-'a'+1;
            if(valueTable.count(s[i])) value = valueTable[s[i]];
            dp[i] = max(dp[i-1]+value, value);
            // 更新全局最大值
            ans = max(ans, dp[i]);
        }
        return ans < 0 ? 0 : ans;
    }
};

时间复杂度：O(n + m)
空间复杂度：O(n + m)

2192. 有向无环图中一个节点的所有祖先

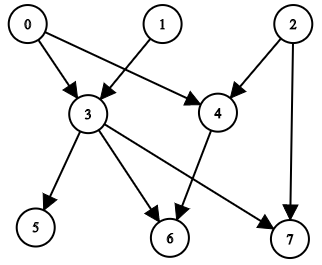
思路：正向 DFS

例如示例 1，从 2 出发 DFS，可以访问到 4,6,7，那么把 2 加到 answer[4]，answer[6]，answer[7] 中。

依次从起点 start=0,1,2,⋯,n−1 出发 DFS，途中把 start 加到能访问到的点的 answer 中。由于 start 从小到大枚举，所以 answer[i] 列表自然就是有序的了。

例如：

从 0 出发访问到 5，把 0 加到 answer[5] 中，现在 answer[5]=[0]。
从 1 出发访问到 5，把 1 加到 answer[5] 中，现在 answer[5]=[0,1]。
从 3 出发访问到 5，把 3 加到 answer[5] 中，现在 answer[5]=[0,1,3]。

小 tips ：正常情况下，每次从父节点出发都要重置 visited 数组，由于题目特性无需每次重置。我们会跑 n 个 DFS，每个 DFS 的 start 都是不同的。利用这一条件，当访问到节点 x 时，标记 vis[x]=start，表示 x 是本轮 DFS 中访问到的节点。当我们访问到某个节点 y 时，如果发现 vis[y]=start，就表示 y 访问过了，否则没有访问过。

class Solution {
public:
    vector<vector<int>> getAncestors(int n, vector<vector<int>>& edges) 
    {
        // 构建邻接表
        vector<vector<int>> adj(n);
        for(auto& edge : edges)
        {
            adj[edge[0]].emplace_back(edge[1]);
        } 
        vector<vector<int>> ans(n);
        vector<int> visited(n,-1);
        // 从小到大遍历，作为祖先
        for(int i = 0; i < n; ++i)
        {
            // 深搜
            dfs(adj, visited, ans, i, i);
        }
        return ans;
    }

    void dfs(vector<vector<int>>& adj, 
    vector<int>& visited, vector<vector<int>>& ans, int ancestor, int n)
    {
        // 标记当前节点的祖先
        visited[n] = ancestor;
        // 遍历当前节点的所有子节点
        for(auto& neighbor : adj[n])
        {
            // 寻找没有祖先和祖先不同的节点
            if(visited[neighbor] != ancestor)
            {
                // 子节点添加祖先
                ans[neighbor].emplace_back(ancestor);
                // 继续深搜
                dfs(adj, visited, ans, ancestor, neighbor);
            }
        }
    }
};

时间复杂度：O(n²)
空间复杂度：O(n²)

2653. 滑动子数组的美丽值

思路：

由于值域很小，所以借鉴计数排序，用一个 cnt 数组维护窗口内每个数的出现次数。然后遍历 cnt 去求第 x 小的数。

什么是第 x 小的数？

设它是 \(num\)，那么 \(<num\) 的数有 \(<x\) 个，\(≤num\) 的数有 \(≥x\) 个，就说明 \(num\) 是第 \(x\) 小的数。

比如 [−1,−1,−1] 中，第 1,2,3 小的数都是 −1。

class Solution {
public:
    vector<int> getSubarrayBeauty(vector<int>& nums, int k, int x) 
    {
        int n = nums.size();
        vector<int> ans;
        // 记录窗口内元素的个数
        vector<int> table(101);
        // 开始滑动
        for(int i = 0; i < n; ++i)
        {
            // 滑动窗口的入口
            table[nums[i]+50]++;
            // 小于窗口大小
            if(i < k-1) continue;
            // 第 x 小的元素的位置应该是 
            // 第一个让 count >= x 的位置
            int count = 0;
            for(int j = 0; j < 101; ++j)
            {
                // 窗口有该元素
                if(table[j] > 0)
                {
                    // 累积元素个数
                    count += table[j];
                    // 第一个让 count >= x 的元素
                    if(count >= x) 
                    {
                        if(j - 50 < 0) ans.emplace_back(j-50);
                        else ans.emplace_back(0);
                        break;
                    }
                }
            }
            // 滑动窗口的出口
            table[nums[i-k+1]+50]--;
        }
        return ans;
    }
};

时间复杂度：O(n)
空间复杂度：O(n)

2080. 区间内查询数字的频率

思路：

对于 arr 中的每个数，计算其在 arr 中的出现位置（下标）。例如 arr=[1,2,1,1,2,2]，其中数字 2 的下标为 [1,4,5]。

知道了下标，那么对于 query 来说，问题就变成了：

下标列表中，满足 \(left≤i≤right\) 的下标 i 的个数。例如 query(3,5,2)，由于数字 2 的下标列表 [1,4,5] 中的下标 4 和 5 都在区间 [3,5] 中，所以返回 2。

把下标列表记作数组 a，由于 a 是有序数组，我们可以用二分查找快速求出：

a 中的第一个 \(≥left\) 的数的下标，设其为 p。如果不存在，则 p 等于 a 的长度。
a 中的第一个 \(>right\) 的数的下标，设其为 q。如果不存在，则 q 等于 a 的长度。

a 中的下标在 [p,q−1] 内的数都是满足要求的，这有 q−p 个。特别地，如果 a 中没有满足要求的下标，那么 q−p=0，这仍然是正确的。

class RangeFreqQuery {
public:
    RangeFreqQuery(vector<int>& arr) 
    {
        int n = arr.size(); 
        // 使用哈希表统计每个元素出现的位置（pos）
        // 由于遍历的顺序，位置已经排序完成
        for(int i = 0; i < n; ++i)
        {
            pos[arr[i]].push_back(i);
        }
    }
    
    int query(int left, int right, int value) 
    {
        if(!pos.count(value)) return 0;
        // 查询 ≤ value 和 ＞ value 的位置
        auto it = lower_bound(pos[value].begin(), pos[value].end(), left);
        auto it_2 = upper_bound(pos[value].begin(), pos[value].end(), right);
        // 两个位置相减即为答案
        return it_2-it;
    }
private:
    unordered_map<int, vector<int>> pos;
};

/**
 * Your RangeFreqQuery object will be instantiated and called as such:
 * RangeFreqQuery* obj = new RangeFreqQuery(arr);
 * int param_1 = obj->query(left,right,value);
 */

查询时间复杂度：O(log m)
空间复杂度：O(n)

962. 最大宽度坡

思路：

首先正序遍历数组 A，将以 A[0] 开始的递减序列的元素下标依次存入栈中。以[6,1,8,2,0,5]为例，由于(6,1,0)是递减的，所以栈中存的元素应该为：\(（栈顶 -> (4,1,0)<-栈底）\)。
此时栈 stack:(4(0), 1(1), 0(6))：然后逆序排列数组 A，若以栈顶元素为下标A[stack.peek()]小于等于当前遍历的元素 A[i]，即 A[stack.peek()] <= A[i]。此时就是一个满足条件的坡的宽度，并且这个宽度一定是栈顶这个坡底 i 能形成的最大宽度，将栈顶元素出栈并计算当前坡的宽度，保留最大值即可。

class Solution {
public:
    int maxWidthRamp(vector<int>& nums) 
    {
        int n = nums.size();
        // 利用单调栈寻找严格递减序列
        stack<int> stk;
        for(int i = 0; i < n; ++i)
        {
            if(stk.empty() || nums[stk.top()] > nums[i]) stk.emplace(i);
        }

        int ans = INT_MIN;
        // 贪心-比较当前值和 stack 堆顶的大小
        for(int j = n-1; j >= 0; --j)
        {
            while(!stk.empty() && nums[j] >= nums[stk.top()])
            {
                ans = max(ans, j-stk.top());
                stk.pop();
            }
        }
        return ans;
    }
};

时间复杂度：O(n)
空间复杂度：O(n)

1749. 任意子数组和的绝对值的最大值

思路 1：动态规划

问题可以转换成求 53. 最大子数组和以及「最小子数组和的绝对值（相反数）」，这二者中的最大值就是答案。

考虑以 nums[i] 结尾的最大子数组和：

如果子数组只有一个数，那么最大子数组和就是 nums[i]。
如果把 nums[i] 和前面的子数组拼起来，那么问题变成求「以 nums[i−1] 结尾的最大子数组和」。

这启发我们得到下面的状态定义和状态转移方程。

定义 f[i] 表示以 nums[i] 结尾的最大子数组和：

如果子数组只有一个数：f[i]=nums[i]。如果把 nums[i] 和前面的子数组拼起来：f[i]=f[i−1]+nums[i]。这两种情况取最大值，即 \[ f[i]=max(nums[i],f[i−1]+nums[i])=max(f[i−1],0)+nums[i] \] 枚举子数组的最后一个数，最大子数组和就是 \[ max(max(f),0) \] 这里与 0 取最大值是因为子数组可以为空。

最小子数组和的计算方法与最大子数组和类似。

class Solution {
public:
    int maxAbsoluteSum(vector<int>& nums) 
    {
        int n = nums.size();
        int maximum = 0, minimum = 0, ans = 0;
        for(int i = 0; i < n; ++i)
        {
            // 以 nums[i] 结尾的最大子数组和
            maximum = max(maximum, 0) + nums[i];
            // 以 nums[i] 结尾的最小子数组和
            minimum = min(minimum, 0) + nums[i];
            // 每次更新最大值，就不用最后遍历寻找最大值
            ans = max(ans, max(abs(minimum), abs(maximum)));
        }    
        return ans;
    }
};

时间复杂度：O(n)。
空间复杂度：O(1)。

思路 2：前缀和

设 nums 的前缀和数组为 s，根据前置知识，子数组的和等于两个前缀和的差 s[j]−s[i]。所以子数组和的绝对值等于

\[ ∣s[j]−s[i]∣ \] s[i] 和 s[j] 相差越大，上式也就越大。

给你一堆数，哪两个数相差最大？这堆数字中的最大值和最小值相差最大。

所以，最大的差来自 s 中的最大值和最小值，所以答案为

\[ max(s)−min(s) \] 你也可以这样理解：

如果最大前缀和在最小前缀和的右边，那么上式算的是最大子数组和。
如果最大前缀和在最小前缀和的左边，那么上式算的是最小子数组和的绝对值。最小的负数取绝对值可以得到最大的正数。

class Solution {
public:
    int maxAbsoluteSum(vector<int>& nums) 
    {
        int n = nums.size();
        // 求 最大前缀和 和 最小前缀和 差的 最大值和最小值    
        vector<int> preSum(n);
        preSum[0] = nums[0];
        for(int i = 1; i < n; ++i)
        {
            preSum[i] = preSum[i-1] + nums[i];
        }

        auto it = max_element(preSum.begin(), preSum.end());
        auto it_2 = min_element(preSum.begin(), preSum.end());

        return max({abs(*it-*it_2), abs(*it), abs(*it_2)});
    }
};

优化版本：

class Solution {
public:
    int maxAbsoluteSum(vector<int>& nums) 
    {
        // 如果最大值小于0，则 mx = 0，返回 -mn
        // 如果最小值大于0，则 mn = 0，返回 mx
        int s = 0, mx = 0, mn = 0;
        for (int x : nums) 
        {
            // 计算前缀和
            s += x;
            // 更新前缀和最大值
            mx = max(mx, s);
            // 更新前缀和最小值
            mn = min(mn, s);
        }
        return mx - mn;
    }
};

时间复杂度：O(n)
空间复杂度：O(1)

3387. 两天自由外汇交易后的最大货币数

思路：

根据 pairs1 和 rates1 建图。
从 initialCurrency 开始，自顶向下 DFS 这张图，递归的同时维护金额。记录把initialCurrency 兑换成其他货币的金额 day1Amount。
根据 pairs2 和 rates2 建图。
同样地，从 initialCurrency 开始，自顶向下 DFS 这张图，递归的同时维护金额。记录把 initialCurrency 兑换成其他货币的金额 day2Amount。金额的倒数，就是从其他货币兑换成 initialCurrency 的金额。

枚举中转货币 x，答案为 \(\frac{day2Amount[x]}{day1Amount[x]}\) 的最大值。

class Solution {
public:
    double maxAmount(string initialCurrency, vector<vector<string>>& pairs1, vector<double>& rates1, vector<vector<string>>& pairs2, vector<double>& rates2) 
    {
        // 深搜 计算第一天将 initialCurrency 转换为 targetCurrency 的结果
        unordered_map<string, vector<pair<string, double>>> adj1;
        buildAdj(pairs1, rates1, adj1);
        unordered_map<string, double> amount_1;
        dfs(adj1, amount_1, 1.0, initialCurrency);
        // 深搜 计算第二天将 initialCurrency 转换为 targetCurrency 的结果
        unordered_map<string, vector<pair<string, double>>> adj2;
        buildAdj(pairs2, rates2, adj2);
        unordered_map<string, double> amount_2;
        dfs(adj2, amount_2, 1.0, initialCurrency);

        // 查找两天相同的 targetCurrency 寻找最大值
        double ans = 0;
        for(auto& [key_1, value_1] : amount_1)
        {
            for(auto& [key_2, value_2] : amount_2)
            {
                if(key_1 == key_2)
                {
                    ans = max(ans, value_1/value_2);
                }
            }
        }
        return ans;
    }

    // 使用哈希表构建邻接表
    void buildAdj(vector<vector<string>>& pairs, vector<double>& rates, unordered_map<string, vector<pair<string, double>>>& adj)
    {
        int n = pairs.size();
        for(int i = 0; i < n; ++i)
        {
            adj[pairs[i][0]].emplace_back(pairs[i][1], rates[i]);
            adj[pairs[i][1]].emplace_back(pairs[i][0], 1/rates[i]);
        }
    }

    // 深搜
    void dfs(unordered_map<string, vector<pair<string, double>>>& adj, unordered_map<string, double>& amount, double currentAmount, string current)
    {
        amount[current] = currentAmount;
        // 当前货币没有 targetCurrency 则递归终止
        if(!adj.count(current)) return;
        // 遍历当前货币的所有 targetCurrency
        for(auto& [neighbor, rate] : adj[current])
        {
            // 如果 未遍历该货币 则递归搜索
            if(!amount.count(neighbor))
            {
                dfs(adj, amount, currentAmount*rate, neighbor);
            }
        }
    }
};

时间复杂度：O((n+m)L)，其中 n 是 pairs1的长度，m 是 pairs2的长度，L 是单个字符串的长度（不超过 3）。
空间复杂度：O((n+m)L)。

每周LeetCode回顾-1

456. 132模式

思路：

189. 轮转数组

思路：

73. 矩阵置零

思路：

238. 除自身以外数组的乘积

思路：

2134. 最少交换次数来组合所有的 1 II

思路：

1297. 子串的最大出现次数

思路：

2389. 和有限的最长子序列

思路：

2140. 解决智力问题

思路：

一、寻找子问题

二、状态定义与递推公式

53. 最大数组和

思路 1：前缀和 + 贪心

思路 2：动态规划

动态规划定义